Khan Academy on a Stick
Multiplicando y factorizando expresiones
Este tema va a añadir un montón de herramientas a tu caja de herramientas algebraica. Serás capaz de multiplicar cualquier expresión y aprender a factorizar muchisimas de ellas. Esto te permitirá resolver una amplia gama de problemas de álgebra.
-
 Factorizando Productos Especiales
(ES)
Factorizando Productos Especiales
(ES)
Factorizando Productos Especiales
-
 Ejemplo 1: Factorizando diferencia de cuadrados
(ES)
cc
Ejemplo 1: Factorizando diferencia de cuadrados
(ES)
ccFactorizando diferencia de cuadrados
-
 Ejemplo 2: Factorizando una diferencia de cuadrados
(ES)
cc
Ejemplo 2: Factorizando una diferencia de cuadrados
(ES)
ccFactorizando diferencia de cuadrados
-
 Factorización para producir diferencias de cuadrados
(EN)
Factorización para producir diferencias de cuadrados
(EN)
-
 Ejemplo: Factorizando trinomios cuadrados perfectos
(ES)
Ejemplo: Factorizando trinomios cuadrados perfectos
(ES)
Factorizando trinomios cuadrados perfectos
-
 Ejemplo: Factorizando una expresión de cuarto grado
(ES)
Ejemplo: Factorizando una expresión de cuarto grado
(ES)
Factorizando Productos Especiales 2
-
 Ejemplo: Factorizando productos notables
(ES)
cc
Ejemplo: Factorizando productos notables
(ES)
ccFactorizando Productos Especiales 1
Factorización de productos especiales
Encontrarás cuadráticas factorizables que no lo parecen. Este tutorial extenderá tu arsenal de herramientas a través de la exposición de los productos especiales, la diferencia de cuadrados y los cuadrados perfectos.
-
 Multiplicando Monomios
(ES)
Multiplicando Monomios
(ES)
Multiplicando Monomios
-
 Dividiendo Monomios
(ES)
Dividiendo Monomios
(ES)
Dividiendo Monomios
-
 Multiplicando y Dividiendo Monomios 1
(EN)
Multiplicando y Dividiendo Monomios 1
(EN)
Multiplicando y Dividiendo Monomios 1
-
 Multiplicando y Dividiendo Monomios 2
(ES)
Multiplicando y Dividiendo Monomios 2
(ES)
Multiplicando y Dividiendo Monomios 2
-
 Multiplicando y Dividiendo Monomios 3
(ES)
Multiplicando y Dividiendo Monomios 3
(ES)
Multiplicando y Dividiendo Monomios 3
-
 Monomio Máximo Común Divisor
(ES)
Monomio Máximo Común Divisor
(ES)
Monomio Máximo Común Divisor
Multiplicando y dividiendo monomios
"Monomios" suena como una palabra elegante y rara, pero sólo se refiere a los términos individuales como "4x" o "8xy" o "17x^2z". En este tutorial aprenderemos a multiplicarlos y dividirlos usando ideas que ya te resultan familiares (como las propiedades de los exponentes y el máximo común divisor).
-
 Problema escrito de multiplicación de binomios
(ES)
Problema escrito de multiplicación de binomios
(ES)
Problema escrito de multiplicación de binomios
-
 Método FOIL o de la hoja para multiplicar binomios
(ES)
Método FOIL o de la hoja para multiplicar binomios
(ES)
Método FOIL o de la hoja para multiplicar binomios
-
 Multiplicando binomios con radicales
(ES)
Multiplicando binomios con radicales
(ES)
Multiplicando binomios con radicales
-
 Multiplicando binomios ejemplo 1
(ES)
Multiplicando binomios ejemplo 1
(ES)
Multiplicando binomios
-
 Ejemplo 2 del método FOIL o de la hoja para multiplicar binomios
(ES)
Ejemplo 2 del método FOIL o de la hoja para multiplicar binomios
(ES)
Ejemplo 2 del método FOIL o de la hoja para multiplicar binomios
-
 Cuadrado de un binomio
(ES)
Cuadrado de un binomio
(ES)
Cuadrado de un binomio
-
 Productos Especiales de Binomios
(ES)
cc
Productos Especiales de Binomios
(ES)
ccProductos Especiales de Binomios
-
 Multiplicación de binomios para obtener la diferencia de cuadrados
(ES)
Multiplicación de binomios para obtener la diferencia de cuadrados
(ES)
Multiplicación de binomios para obtener la diferencia de cuadrados
-
 Haciendo el cuadrado de un binomio
(ES)
Haciendo el cuadrado de un binomio
(ES)
Haciendo el cuadrado de un binomio
-
 Haciendo el cuadrado de un binomio ejemplo 2
(ES)
Haciendo el cuadrado de un binomio ejemplo 2
(ES)
Haciendo el cuadrado de un binomio ejemplo 2
-
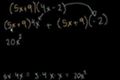 Video clásico de multiplicación de binomios
(ES)
cc
Video clásico de multiplicación de binomios
(ES)
cc(Ax+By)(Ax+By)
Multiplicando binomios
En este tutorial aprenderás que multiplicar cosas como (4x-7)(-9x+5) requiere unicamente de la propiedad distributiva que aprendiste en la escuela primaria. Te iniciaremos en el método FOIL porque parece estar cubierto en muchas escuelas, pero no nos gusta (no creemos que sea bueno memorizar los procesos sin saber el por qué).
-
 Factorización y la Propiedad Distributiva 3
(ES)
Factorización y la Propiedad Distributiva 3
(ES)
Factorización y la Propiedad Distributiva 3
-
 Factorizando binomios lineales
(EN)
Factorizando binomios lineales
(EN)
-
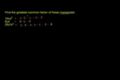 Factorización y la Propiedad Distributiva
(EN)
Factorización y la Propiedad Distributiva
(EN)
Factorización y la Propiedad Distributiva
-
 Factorización y la Propiedad Distributiva 2
(ES)
Factorización y la Propiedad Distributiva 2
(ES)
Factorización y la Propiedad Distributiva 2
-
 Factorización de expresiones utilizando el MFC
(ES)
Factorización de expresiones utilizando el MFC
(ES)
Factorización de expresiones utilizando el MFC
Factorizando expresiones simples
Ya sabes un poco sobre la multiplicación de expresiones. Ahora vamos a ir hacia atrás y a pensar en una expresión como el producto de otras expresiones más simples (como le hicimos cuando encontramos los factores de un número).
-
 Factorizando expresiones cuadráticas
(ES)
cc
Factorizando expresiones cuadráticas
(ES)
ccFactorizando Expresiones Cuadráticas
-
 Ejemplos: Factorizando cuadráticas simples
(ES)
Ejemplos: Factorizando cuadráticas simples
(ES)
Algunos ejemplos de factorización de cuadráticas
-
 Ejemplo 1: Factorizando de expresiones cuadráticas
(ES)
Ejemplo 1: Factorizando de expresiones cuadráticas
(ES)
Factorizando trinomios con 1 coeficiente líder
-
 Ejemplo 1: Factorizando trinomios con un factor común
(ES)
Ejemplo 1: Factorizando trinomios con un factor común
(ES)
Factorizando trinomios con factor común
Factorizando expresiones cuadráticas
Factorizar ecuaciones cuadráticas (esencialmente polinomios de segundo grados) no sólo es divertido, sino que es bueno para ti. Te permitirá analizar y resolver toda una serie de ecuaciones. Te permitirá impresionar a la gente en las fiestas y subir peldaños en la escalera de tu carrera. ¡Qué emocionante!
-
 Factorizando por Agrupación y Factoring Completamente
(ES)
Factorizando por Agrupación y Factoring Completamente
(ES)
Factorizando por Agrupación y Factoring Completamente
-
 Ejemplo: Agrupación básica
(ES)
Ejemplo: Agrupación básica
(ES)
Factorizando Trinomios por Agrupación 1
-
 Ejemplo 6: Factorizando por agrupación
(ES)
Ejemplo 6: Factorizando por agrupación
(ES)
Factorizando trinomios sin 1 coeficiente líder por agrupación
-
 Ejemplo 2: Factorizando por agrupación
(ES)
Ejemplo 2: Factorizando por agrupación
(ES)
U09_L1_T2_we2 Factorizando Trinomios por Agrupación 2
-
 Ejemplo 3: Factorizando por agrupación
(ES)
Ejemplo 3: Factorizando por agrupación
(ES)
Factorizando expresiones cuadráticas simples
-
 Ejemplo 4: Factorizando por agrupación
(ES)
Ejemplo 4: Factorizando por agrupación
(ES)
Factorizando Trinomios por Agrupación 4
-
 Ejemplo 5: Factorizando por agrupación
(ES)
Ejemplo 5: Factorizando por agrupación
(ES)
Factorización de Trinomios por Agrupación 5
-
 Ejemplo 6: Factorización por agrupación
(ES)
Ejemplo 6: Factorización por agrupación
(ES)
Factorizando Trinomios por Agrupación 6
Factorizando por agrupación
La factorización por agrupación es probablemente la técnica que la gente no aprende bien. Tu destino no tiene que ser el mismo. En este tutorial observarás cómo la factorización por agrupación puede ser utilizada para factorizar expresiones cuadráticas en donde el coeficiente del término x^2 es distinto de 1
Factorización de cuadráticas en dos variables
Ahora extenderemos la aplicación de nuestras herramientas para factorizar cuadráticas factorizando expresiones con dos varaibles. Como veremos, esto sólo es la extensión de lo que probablemente ya sabes (o al menos sabrás después de trabajar en este tutorial). ¡Adelante!
-
 Términos coeficientes y exponentes en un polinomio
(ES)
Términos coeficientes y exponentes en un polinomio
(ES)
Términos coeficientes y exponentes en un polinomio
-
 Interesante problema de coeficientes de un polinomio
(EN)
Interesante problema de coeficientes de un polinomio
(EN)
Encontrar los coeficientes de un polinómio de grado tres dados 2 raíces y el punto de intersección
-
 Polinomios 1
(ES)
Polinomios 1
(ES)
Polinomios 1
-
 Polinomios 2
(EN)
Polinomios 2
(EN)
Polinomios 2
-
 Evaluando un polinomio en un valor dado
(ES)
Evaluando un polinomio en un valor dado
(ES)
Evaluando un polinomio en un valor dado
-
 Simplifica un polinomio
(ES)
Simplifica un polinomio
(ES)
Trabajando la simplificación de un polinomio
-
 Sumando Polinomios
(ES)
Sumando Polinomios
(ES)
Sumando Polinomios
-
 Ejemplo: Adición de polinomios con muchas variables
(ES)
Ejemplo: Adición de polinomios con muchas variables
(ES)
Ejemplo básico de simplificación de una expresión polinómica con múltiples variables.
-
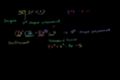 Suma y resta de polinomios
(ES)
Suma y resta de polinomios
(ES)
Suma y resta de polinomios
-
 Sumando y Restando Polinomios 1
(EN)
Sumando y Restando Polinomios 1
(EN)
Sumando y Restando Polinomios 1
-
 Sumando y Restando Polinomios 2
(EN)
Sumando y Restando Polinomios 2
(EN)
Sumando y Restando Polinomios 2
-
 Sumando y Restando Polinomios 3
(EN)
Sumando y Restando Polinomios 3
(EN)
Sumando y Restando Polinomios 3
-
 Restando Polinomios
(ES)
Restando Polinomios
(ES)
Restando Polinomios
-
 Restando polinomios con múltiples variables
(ES)
cc
Restando polinomios con múltiples variables
(ES)
ccRestando polinomios con múltiples variables
Lo básico de los polinomios
"Polinomios" suena como una palabra elegante, pero lo único que tienes que las raices de la palabra. "Poli" significa "muchos". Así que sólo estamos hablando acerca de "muchos nomios" y todo el mundo sabe lo que es un "nomio ". Esta bien, muchos de nosotros no. Bueno, un polinomio tiene "muchos" términos. Desde entender lo que es un "término" a la simplificación básica, suma y resta de polinomios, este tutorial te familiarizará mucho con el mundo de muchos "nomios." :)
-
 Multiplicando Monomios por Polinomios
(ES)
Multiplicando Monomios por Polinomios
(ES)
Multiplicando Monomios por Polinomios
-
 Multiplicando Polinomios
(ES)
Multiplicando Polinomios
(ES)
Multiplicando Polinomios
-
 Multiplicando Polinomios 3
(ES)
Multiplicando Polinomios 3
(ES)
Multiplicando Polinomios 3
-
 Más de multiplicación de polinomios
(ES)
Más de multiplicación de polinomios
(ES)
Más de multiplicación de polinomios
Multiplicando polinomios
En este tutorial veremos que multiplicar polinomios es sólo una extensión de la misma propiedad distributiva que aprendiste al multiplicar expresiones más simples (por eso creemos que el método de FOIL, o método de la hoja, es patético--no generaliza y es más una memorización que una comprensión real).
-
 División de polinomios
(ES)
División de polinomios
(ES)
División de polinomios
-
 Polinomio dividido por un monomio
(ES)
Polinomio dividido por un monomio
(ES)
Polinomio dividido por un monomio
-
 Dividiendo polinomios con múltiples variables por un monomio
(ES)
Dividiendo polinomios con múltiples variables por un monomio
(ES)
Dividiendo polinomios con múltiples variables por un monomio
-
 Dividiendo polinomios 1
(ES)
Dividiendo polinomios 1
(ES)
Dividiendo polinomios 1
-
 Dividiendo polinomios con residuos
(ES)
cc
Dividiendo polinomios con residuos
(ES)
ccDividiendo polinomios con residuos
-
 División Sintética
(ES)
División Sintética
(ES)
Algoritmo básico para la División Sintética
-
 Ejemplo de División Sintética 2
(ES)
Ejemplo de División Sintética 2
(ES)
Otro ejemplo de aplicación del algoritmo básico de la división sintética
-
 Por qué Funciona la División Sintética
(ES)
Por qué Funciona la División Sintética
(ES)
Demostrando por qué la división sintética te da el mismo resultado que la tradicional división algebraica larga
-
 Factorización de suma de cubos
(ES)
Factorización de suma de cubos
(ES)
Factorización de suma de cubos
-
 Factorización de diferencia de cubos
(ES)
Factorización de diferencia de cubos
(ES)
U12 l2 t3 we2 Diferencia de Factorización Cúbica
-
 División Algebraica Larga
(ES)
División Algebraica Larga
(ES)
Dividiendo un polinomio por otro
-
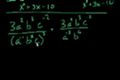 Álgebra II: Simplificando Polinomios
(EN)
cc
Álgebra II: Simplificando Polinomios
(EN)
cc17-22, simplificando polinomios y expresiones algebraicas
Dividiendo polinomios
Tú sabes lo que son los polinomios. Sabes cómo sumar, restar y multiplicarlos. A menos que no tengas nada de curiosidad, te debes estar preguntando cómo dividirlos En este tutorial exploraremos cómo se dividen los polinomios, a través tanto de la división algebráica larga y de la división sintética. A nosotros nos gusta la división algebráica larga más porque puedes entender realmente lo que estás haciendo.
 Factorización de cuadráticas con dos variables
Factorización de cuadráticas con dos variables Factorización de cuadráticas con dos variables - Ejemplo
Factorización de cuadráticas con dos variables - Ejemplo