Khan Academy on a Stick
Graphing linear functions
Usa el poder del álgebra para comprender e interpretar puntos y líneas (algo que normalmente hacemos en geometría). Esto incluirá la pendiente y la ecuación de una línea.
-
 Descartes y las Coordenadas Cartesianas
(ES)
cc
Descartes y las Coordenadas Cartesianas
(ES)
ccTendiendo un puente entre el álgebra y la geometría. Qué hace tan lineal a las ecuaciones lineales.
-
 El Plano Coordenado
(ES)
El Plano Coordenado
(ES)
-
 Trazar pares ordenados
(EN)
cc
Trazar pares ordenados
(EN)
ccTrazar pares ordenados
-
 Cuadrantes en el Plano Coordenado
(EN)
Cuadrantes en el Plano Coordenado
(EN)
Cuadrantes en el Plano Coordenado
Plano cartesiano
¿Cómo podemos comunicar exactamente dónde está algo en dos dimensiones? ¿Quién era este tal Descartes? En este tutorial revisamos las bases del plano cartesiano. Después ahondamos en el graficar de puntos y determinar si un punto es la solución de una ecuación. Este será un gran tutorial si estás empezando a aumentar tu comprensión de las gráficas o necesitas una revisión fundamental.
-
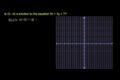 Soluciones par ordenado de ecuaciones
(EN)
Soluciones par ordenado de ecuaciones
(EN)
Parejas ordenadas como solución de ecuaciones
-
 Parejas ordenadas como solución de ecuaciones 2
(EN)
Parejas ordenadas como solución de ecuaciones 2
(EN)
Parejas ordenadas como solución de ecuaciones
-
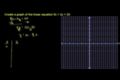 Graficando relaciones (x,y)
(EN)
Graficando relaciones (x,y)
(EN)
Graficando relaciones (x,y)
-
 Gráficas de ecuaciones lineales
(ES)
Gráficas de ecuaciones lineales
(ES)
-
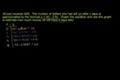 Problema de aplicación con gráficas
(EN)
Problema de aplicación con gráficas
(EN)
Problema de aplicación con gráficas
-
 Interpretando gráficas lineales
(ES)
cc
Interpretando gráficas lineales
(ES)
ccInterpretando gráficas lineales
-
 Explorando relaciones lineales
(EN)
Explorando relaciones lineales
(EN)
Explorando relaciones lineales
-
 Reconociendo Funciones Lineales
(ES)
cc
Reconociendo Funciones Lineales
(ES)
ccReconociendo Funciones Lineales
-
 Graficando rectas 1
(EN)
cc
Graficando rectas 1
(EN)
ccGraficando ecuaciones lineales
Graficando soluciones de ecuaciones
En este tutorial trabajaremos los ejemplos que muestran cómo una línea puede ser vista como todas las coordenadas cuyos valores de x y y satisfacen una ecuación lineal. Asimismo, una ecuación lineal puede ser vista como describiendo una relación entre los valores de x y y de una línea.
-
 Reconociendo Funciones Lineales
(ES)
cc
Reconociendo Funciones Lineales
(ES)
ccReconociendo Funciones Lineales
-
 Funciones lineales y no lineales (ejemplo 1)
(EN)
Funciones lineales y no lineales (ejemplo 1)
(EN)
-
 Funciones lineales y no lineales (ejemplo 2)
(EN)
Funciones lineales y no lineales (ejemplo 2)
(EN)
-
 Funciones lineales y no lineales (ejemplo 3)
(EN)
Funciones lineales y no lineales (ejemplo 3)
(EN)
Funciones lineales y no lineales
No todas las relaciones en el universo pueden ser representadas por una línea (de hecho, casi ninguna). Llamamos a estas relaciones "no lineales". En este tutorial aprenderemos a distinguir entre una función lineal y una no lineal ¡Diviértete!
-
 Gráficas usando los interceptos en X e Y
(ES)
Gráficas usando los interceptos en X e Y
(ES)
Gráficas usando los interceptos en X e Y
-
 Gráficando Usando Intersecciones
(ES)
Gráficando Usando Intersecciones
(ES)
-
 Intersecciones X y Y
(EN)
Intersecciones X y Y
(EN)
Intersecciones X y Y
-
 Intersecciones con los ejes X y Y
(EN)
Intersecciones con los ejes X y Y
(EN)
Intersecciones con los ejes X y Y
-
 Finding x intercept of a line
(EN)
Finding x intercept of a line
(EN)
-
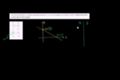 Finding intercepts for a linear function from a table
(EN)
Finding intercepts for a linear function from a table
(EN)
-
 Interpreting intercepts of linear functions
(EN)
Interpreting intercepts of linear functions
(EN)
x-intercepts and y-intercepts of linear functions
Hay muchas formas de graficar una línea y este tutorial cubre una de las más simples. Dado que sólo necesitas dos puntos para formar una línea, encontremos qué valor el valor que una ecuación toma en x = 0 (en esencia la ordenada al origen), y qué valor toma cuando Y = 0 (la abscisa al origen). Después podemos graficar la línea yendo a través de los dos puntos.
Relaciones proporcionales y tasas de cambio
En este tutorial vamos a pensar más profundamente en cómo cambia una variable con respecto a otra. Presta mucha atención porque vas a encontrar que estas ideas ¡seguirán apareciendo a través de tu vida!
-
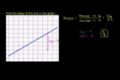 Pendiente de una recta
(ES)
cc
Pendiente de una recta
(ES)
ccPendiente de una recta
-
 Pendiente de una Recta 2
(ES)
cc
Pendiente de una Recta 2
(ES)
ccPendiente de una Recta 2
-
 Pendiente y Razón de Cambio
(ES)
Pendiente y Razón de Cambio
(ES)
-
 Gráfica de la pendiente de una recta
(ES)
Gráfica de la pendiente de una recta
(ES)
Gráfica de la pendiente de una recta
-
 Pendiente de una Recta 3
(ES)
Pendiente de una Recta 3
(ES)
Pendiente de una Recta 3
-
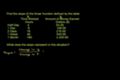 Ejemplo de la pendiente
(ES)
Ejemplo de la pendiente
(ES)
Ejemplo de la pendiente
-
 Pendiente de la Recta Peluda
(ES)
Pendiente de la Recta Peluda
(ES)
Horripilante pendiente de una línea
-
 Promedio de tasa de cambio ejemplo 2)
(EN)
Promedio de tasa de cambio ejemplo 2)
(EN)
-
 Promedio de tasa de cambio ejemplo 3)
(EN)
Promedio de tasa de cambio ejemplo 3)
(EN)
-
 Álgebra: Pendiente
(ES)
cc
Álgebra: Pendiente
(ES)
ccEncontrando la pendiente de una recta
-
 Álgebra: Pendiente 2
(EN)
cc
Álgebra: Pendiente 2
(EN)
ccSegunda parte de la determinación de la pendiente de una recta
-
 Álgebra: Pendiente 3
(EN)
cc
Álgebra: Pendiente 3
(EN)
ccParte 3 de pendiente
Pendiente
Si alguna vez te ha costado trabajo decirle a alguien lo espinado que una cosa es, encontrarás la respuesta aquí. En este tutorial revisamos la idea de la pendiente de una recta. También reflexionamos acerca de cómo la pendiente se relaciona con la ecuación de una recta y cómo puedes determinar la pendiente o la ordenada al origen dadas algunas pistas. Este tutorial es apropiado para alguien que entiende las bases de la graficación de ecuaciones y quiere profundizar un poco más. Después de este tutorial estarás preparado para empezar a pensar más acerca de la ecuación de una recta.
-
 Graficando una recta en la forma pendiente- ordenada al origen
(ES)
cc
Graficando una recta en la forma pendiente- ordenada al origen
(ES)
ccGraficando una recta en la forma pendiente- ordenada al origen
-
 Conversión a la forma pendiente-intercepto
(ES)
Conversión a la forma pendiente-intercepto
(ES)
Conversión a la forma pendiente-intercepto
-
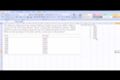 Ajustando una línea a los datos
(EN)
Ajustando una línea a los datos
(EN)
Gráficas de ecuaciones lineales en la forma pendiente-intersección
Las Matemáticas son bellas porque hay muchas maneras de apreciar la misma relación. En este tutorial utilizaremos nuestros conocimientos de la pendiente para graficar líneas que han sido expresadas en la forma pendiente-intersección.
-
 Comparando funciones lineales 1
(EN)
Comparando funciones lineales 1
(EN)
-
 Comparando funciones lineales 2
(EN)
Comparando funciones lineales 2
(EN)
-
 Comparando funciones lineales 3
(EN)
Comparando funciones lineales 3
(EN)
-
 Interpreting features of linear functions example 2
(EN)
Interpreting features of linear functions example 2
(EN)
-
 Aplicaciones de Comparando funciones lineales 2
(EN)
Aplicaciones de Comparando funciones lineales 2
(EN)
-
 Aplicaciones de Comparando funciones lineales 3
(EN)
Aplicaciones de Comparando funciones lineales 3
(EN)
-
 Constructing a linear function word problem
(EN)
Constructing a linear function word problem
(EN)
-
 Constructing and interpreting a linear function
(EN)
Constructing and interpreting a linear function
(EN)
Analizando funciones lineales
Las funciones lineales aparecen a lo largo de la vida (incluso aunque no te des cuenta). Este tutorial te hará pensar mucho más profundamente acerca del significado de una función lineal y varias de las formas de interpretar una. Como siempre, pausa el video y trata de resolver el problema antes que Sal. Después practica tu conocimiento y practica resolviendo los problemas al final del tutorial.
-
 Ejemplos múltiples de construcción de ecuaciones lineales en la forma pendiente-intersección
(ES)
Ejemplos múltiples de construcción de ecuaciones lineales en la forma pendiente-intersección
(ES)
Ecuaciones lineales y la forma pendiente-intersección
-
 Construcción de ecuaciones en la forma pendiente-intersección a partir de gráficas
(ES)
Construcción de ecuaciones en la forma pendiente-intersección a partir de gráficas
(ES)
-
 Construcción de ecuaciones lineales para resolver problemas escritos
(ES)
cc
Construcción de ecuaciones lineales para resolver problemas escritos
(ES)
ccConstrucción de ecuaciones lineales para resolver problemas escritos
-
 Ecuación lineal en la forma pendiente y un punto
(ES)
Ecuación lineal en la forma pendiente y un punto
(ES)
Ecuación de la línea
-
 Encontrando la ecuación lineal dados un punto y la pendiente
(ES)
Encontrando la ecuación lineal dados un punto y la pendiente
(ES)
Ecuación de la línea 2
-
 Ecuación de la línea a partir de pendiente fraccionaria y un punto
(ES)
Ecuación de la línea a partir de pendiente fraccionaria y un punto
(ES)
u13 l2 t2 we INT Ejemplo peliagudo con la ecuación de la línea
-
 Construcción de la ecuación de una línea a partir de dos puntos
(ES)
Construcción de la ecuación de una línea a partir de dos puntos
(ES)
Ecuación de la línea 3
-
 Encontrando la intersección a partir de la pendiente y un punto
(EN)
Encontrando la intersección a partir de la pendiente y un punto
(EN)
Cosntrucción de ecuaciones en la forma pendiente-intersección
Ya conoces un poco de la pendiente y las intersecciones. Ahora profundizaremos este conocimiento aún más para construir la ecuación de la línea en la forma pendiente-intersección.
-
 La idea detrás de la forma punto-pendiente
(EN)
La idea detrás de la forma punto-pendiente
(EN)
-
 Sistemas de ecuaciones lineales de la forma punto pendiente
(ES)
Sistemas de ecuaciones lineales de la forma punto pendiente
(ES)
Sistemas de ecuaciones lineales de la forma punto pendiente
-
 Ecuaciones lineales en Forma Estándar
(ES)
cc
Ecuaciones lineales en Forma Estándar
(ES)
ccEcuaciones lineales en Forma Estándar
-
 Punto pendiente y forma estándar
(ES)
Punto pendiente y forma estándar
(ES)
Punto pendiente y forma estándar
-
 Conversión de la forma punto-pendiente a pendiente-intersección
(EN)
Conversión de la forma punto-pendiente a pendiente-intersección
(EN)
Pendiente-intersección y la forma estándar
Ya conoces la pendiente en un punto de una línea. Bueno, en este tutorial ahora observarás que rápidamente puedes tomar esta información (y el conocimiento de qué es la pendiente) ¡para construir la ecuación de ésta línea en la forma pendiente-intersección! También realizarás manipulaciones entre las formas punto-pendiente, pendiente-intersección y la forma estándar.
-
 Fórmula de Punto Medio
(EN)
Fórmula de Punto Medio
(EN)
Fórmula de Punto Medio
-
 La introducción a Teorema de Pitágoras
(ES)
La introducción a Teorema de Pitágoras
(ES)
Introducción al teorema de Pitágoras
-
 Fórmula para la Distancia
(ES)
Fórmula para la Distancia
(ES)
Cómo encontrar la distancia entre líneas utilizando la fórmula de Pitágoras
-
 Pendiente de la Línea Perpendicular
(EN)
Pendiente de la Línea Perpendicular
(EN)
Pendiente de línea Perpendicular u13 l2 t3 we1
-
 Ecuaciones de líneas paralelas y perpendiculares
(EN)
Ecuaciones de líneas paralelas y perpendiculares
(EN)
Ecuaciones de líneas paralelas y perpendiculares
-
 Ecuación de la Línea Paralela
(EN)
Ecuación de la Línea Paralela
(EN)
Ecuación de la Línea Paralela
-
 Líneas Paralelas
(EN)
cc
Líneas Paralelas
(EN)
ccLíneas Paralelas
-
 Líneas Paralelas 2
(ES)
Líneas Paralelas 2
(ES)
Líneas Paralelas 2
-
 Líneas paralelas 3
(ES)
Líneas paralelas 3
(ES)
Líneas paralelas 3
-
 Líneas perpendiculares
(ES)
Líneas perpendiculares
(ES)
Líneas perpendiculares
-
 Líneas perpendiculares 2
(EN)
Líneas perpendiculares 2
(EN)
Líneas perpendiculares 2
-
 Distancia entre un punto y una línea
(EN)
Distancia entre un punto y una línea
(EN)
-
 Álgebra: Ecuación de la Recta
(ES)
cc
Álgebra: Ecuación de la Recta
(ES)
ccDeterminando la ecuación de una recta
-
 CA Álgebra I: pendiente y punto de intersección con Y
(ES)
cc
CA Álgebra I: pendiente y punto de intersección con Y
(ES)
cc27-32, encontrando la pendiente, la ordenada al orígen y la ecuación de una recta
Más geometría analítica
Estás familiarizado con las gráficas de rectas, pendientes y ordenadas al origen. Ahora vamos a ir más lejos dentro de la geometría analítica pensando acerca de distancias entre dos puntos, puntos medios, rectas paralelas y perpendiculares. ¡Disfrútalo!
-
 Graficando desigualdades
(ES)
Graficando desigualdades
(ES)
Graficando desigualdades
-
 Resolver y graficar desigualdades lineales con dos variables 1
(EN)
Resolver y graficar desigualdades lineales con dos variables 1
(EN)
Resolver y graficar desigualdades lineales con dos variables
-
 Graficando Inecuaciones Lineales con Dos Variables Ejemplo 2
(ES)
Graficando Inecuaciones Lineales con Dos Variables Ejemplo 2
(ES)
Graficando Inecuaciones Lineales con Dos Variables
-
 Graficando Desigualdades 2
(ES)
Graficando Desigualdades 2
(ES)
Graficando Desigualdades 2
-
 Graficando inecuaciones lineales con dos variables 3
(ES)
cc
Graficando inecuaciones lineales con dos variables 3
(ES)
ccGraficando desigualdades lineales con dos variables
-
 Graficando Desigualdades 1
(ES)
Graficando Desigualdades 1
(ES)
Graficando desigualdades
-
 CA Álgebra I: graficando las desigualdades
(EN)
cc
CA Álgebra I: graficando las desigualdades
(EN)
cc21-26, graficando las desigualdades y probando las afirmaciones
Graficando desigualdades lineales
En este tutorial veremos como graficar desigualdades en el plano cartesiano. También aprenderemos cómo determinar si un punto en particular es una solución de una desigualdad.
Triángulos semejantes y pendiente constante
Usa los triángulos semejantes para explicar por qué una pendiente m es la misma entre dos puntos cualquiera en una línea no vertical en el plano de coordenadas. Vamos a conectar esta idea con la ecuación y = mx (para una línea que para por el origen) y la ecuación y = mx + b (para una línea que intercepta el eje vertical en b) (cc.8.ee.6).
 Problema de velocidad con fracciones 1
Problema de velocidad con fracciones 1 Costo unitario con fracciones 1
Costo unitario con fracciones 1 Comparando relaciones proporcionales
Comparando relaciones proporcionales Construyendo una ecuación para una relación proporcional
Construyendo una ecuación para una relación proporcional Uso de triángulos semejantes para probar que la pendiente de una línea es constante
Uso de triángulos semejantes para probar que la pendiente de una línea es constante