Khan Academy on a Stick
Números imaginarios y números complejos
Ententiendiendo i y el plano complejo
-
 Introducción a i y a los Números Imaginarios
(ES)
cc
Introducción a i y a los Números Imaginarios
(ES)
ccIntroducción a i y a los números imaginarios
-
 Calculando i elevado a Exponentes Arbitrarios
(ES)
cc
Calculando i elevado a Exponentes Arbitrarios
(ES)
ccCalculando i elevada a exponentes arbitrariamente grandes
-
 Raíces Imaginarias de Números Negativos
(ES)
Raíces Imaginarias de Números Negativos
(ES)
Raíces Imaginarias de Números Negativos
-
 i como la Raíz Principal de -1 (un poco técnico)
(ES)
cc
i como la Raíz Principal de -1 (un poco técnico)
(ES)
cci como la raíz cuadrada principal de -1
La unidad imaginaria i
Aquí es donde las Matemáticas comienzan a ponerse geniales. Puede parecer extraño definir un número cuyo cuadrado es negativo ¿Por qué hacemos esto? Porque se crea un sitio agradable en el ecosistema de las matemáticas y porque puede utilizarse para resolver problemas en Ingeniería y Ciencias (sin mencionar que algunos de los fractales más bellos se basan en números imaginarios y complejos). Mientras más lo piensas, puede que te des cuenta que todos los números, no sólo i, son muy abstractos.
-
 Números complejos
(ES)
cc
Números complejos
(ES)
ccNúmeros Complejos
-
 Números Complejos (parte 1)
(ES)
cc
Números Complejos (parte 1)
(ES)
ccIntroducción a los números completos. Sumando, restando y multiplicando números complejos.
-
 Números Complejos (parte 2)
(ES)
Números Complejos (parte 2)
(ES)
Dividiendo números complejos. Complejos conjugados
-
 Sumando Números Complejos
(ES)
Sumando Números Complejos
(ES)
Sumando Números Complejos
-
 Restando Números Complejos
(ES)
Restando Números Complejos
(ES)
Restando Números Complejos
-
 Multiplicando Números Complejos
(ES)
Multiplicando Números Complejos
(ES)
Multiplicando Números Complejos
-
 Dividiendo Números Complejos
(ES)
Dividiendo Números Complejos
(ES)
Dividiendo Números Complejos
-
 Complejos conjugados
(ES)
Complejos conjugados
(ES)
Complejos conjugados
-
 Ejemplo de Complejos Conjugados
(ES)
Ejemplo de Complejos Conjugados
(ES)
Complejos conjugados
Números complejos
Vamos a comenzar a construir números que tengan una parte real y una imaginaria. Los llamaremos números complejos. Podemos incluso graficarlos en el plano complejo y usarlos para encontrar las raíces de CUALQUIER ecuación. ¡La diversión nunca termina!
-
 Análisis Complejo Básico
(ES)
Análisis Complejo Básico
(ES)
Diagrama de Argand, magnitud, módulo y argumento de la forma exponencial
-
 Forma exponencial para encontrar raices complejas
(ES)
Forma exponencial para encontrar raices complejas
(ES)
Usando la forma exponencial para encontrar raíces complejas
-
 Complejos conjugados
(ES)
Complejos conjugados
(ES)
Complejos conjugados
Introducción al análisis complejo
Ya sabes lo que son los números complejos e imaginarios, pero queremos comenzar a escavar un poco más profundo.
-
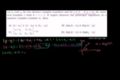 IIT JEE (parte 1) Números Complejos
(ES)
IIT JEE (parte 1) Números Complejos
(ES)
2010 IIT JEE Documento1 Problema 39 Números Complejos (parte 1)
-
 IIT JEE Números Complejos (parte 2)
(ES)
IIT JEE Números Complejos (parte 2)
(ES)
2010 IIT JEE Documento1 Problema 39 Números Complejos (parte 1)
-
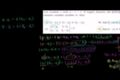 IIT JEE Números Complejos (parte 3)
(ES)
IIT JEE Números Complejos (parte 3)
(ES)
2010 IIT JEE Documento1 Problema 39 Números Complejos (parte 1)
-
 Ejemplo de Determinante Complejo
(ES)
Ejemplo de Determinante Complejo
(ES)
2010 IIT JEE Documento 1 Problema 53 Determinante Complejo
Problemas desafiante con números complejos
Este tutorial aborda un problema especial del IIT JEE de India (exámenes de admisión para entrar en las escuelas de ingeniería). Ya sea que vivas o no en la India, es un buen ejemplo para probar si usted es una estrella de rock de los número complejos.