Khan Academy on a Stick : Sólidos en revolución

Khan Academy on a Stick

Cálculo

Método de disco alrededor del eje-x (ES)
Encontrando el sólido de revolución (construído al rotar alrededor del eje-x) usando el método de discos.
Generalizar el método de disco alrededor del eje x (ES)
Generalizar lo que hicimos en el último video para que f(x) para obtener la "formula" al usar el método de disco alrededor del eje x
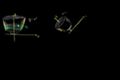Método de discos alrededor del eje-y (ES)
Encontrando el volumen de una figura que es rotada alrededor del eje-y utilizando el método de discos
Método de discos (método de arandela) para la rotación alrededor del eje x (ES)
Encontrar el volumen de un sólido de revolución que está definido entre dos funciones
Generalizando el método de arandelas (ES)
Observando el ejemplo del último video de una manera generalizada
Método de disco de rotación alrededor de una linea horizontal (ES)
Construcción de un sólido de revolución girando alrededor de una línea que no es eje
El método de la arandela giratoria alrededor de ningún eje (ES)
El método de la arandela giratoria al rotar sobre una línea que no sea el eje-x
Parte 2 de arandelas giratorias sin rotación de ejes (ES)
Hacer un poco de álgebra y aritmética complicada para evaluar el integral definido de el último video
Método de disco rotando alrededor de una linea vertical (ES)
Volumen de sólido creado girando alrededor de la línea vertical que no es el eje y usando el método de discos.
Calculando la integral del método de los discos alrededor de una línea vertical (ES)
Calculemos la integral del video anterior.
Método de arandela o anillo para la rotación de línea vertical (ES)
Configuración de la integral definida para el volumen de un sólido de revolución alrededor de una línea vertical mediante el método de "arandelas" o "anillo".
Evaluación de una integral por el método de la arandela alrededor de una linea vertical (ES)
Evaluación de una integral conjunta en el último video usando el método de arandela.

Método del disco

Ya sabes usar integrales definidas para encontrar el área bajo la curva. Ahora tomamos esa idea de "giro" para pensar sobre los volúmenes que se generan cuando giras funciones alrededor de varias líneas. Este tutorial se centra en el "método de discos" y el "método de los anillos" para este tipo de problemas.

Método de cascarones para la rotación alrededor de una línea vertical (ES)
Introduciendo el método de cascarones para la rotación alrededor de una línea vertical.
Evaluación de una integral por el método de cáscaras ejemplo (ES)
Evaluación de una integral definida conjunta usando el método de cáscaras
Método de cascarones para girar alrededor de una línea horizontal (ES)
Ejemplo que muestra cómo encontrar el volumen de un sólido de revolución (construido por rotación alrededor del eje x) usando el método de cascarones (esto podría haberse realizado con el método de discos también).
Método de cascarones con dos funciones de x (ES)
Utiilzando el método de cascarones para rotar alrededor de una línea vertical.
Calculando la integral con el método de cascarones (ES)
Evaluación de una integral conjunta con el método de cáscaras por dos funciones.
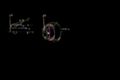Método de cascarones con dos funciones de y (ES)
Parte 2 del método de cascarones con 2 funciones en y (ES)

Método de las arandelas

Si quieres rotar una función alrededor de una línea vertical, pero hacer todos los términos de integración en términos de x y f (x), entonces el método de las arandelas es tu nuevo amigo. Es igualmente fantástico cuando quieres rotar alrededor de una línea horizontal pero integrar en términos de y.

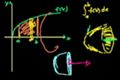Método de discos: función que rota alrededor del eje-x (ES)
cc

Averiguando el volumen de una función girada alrededor del eje x.
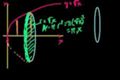Método de disco (rotación f(x) sobre el eje x) (ES)
cc

El volumen de y=sqrt(x) entre x=0 y x=1 rota alrededor del eje x
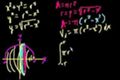Volumen de una esfera (ES)
cc

Descifrando la ecuación del volumen de una esfera.
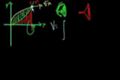Método de discos con fronteras internas y externas (ES)
cc

Más volúmenes alrededor del eje-x.
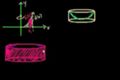Método de cascarones para la rotar alrededor del eje-y (ES)
cc

Usando el método de cascarones para la rotar alrededor del eje-y
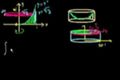Método de discos: rotando x=f(y) alrededor del eje-y (ES)
cc

Usando el método de discos alrededor del eje y.
Método de cascarones alrededor de una línea no eje (ES)
cc

Revoluciones alrededor de algo distinto a alguno de los ejes.
Método de cascarones alrededor de una línea no eje 2 (ES)
cc

La última parte del problema en la parte 7

Volumen de sólido de revolución

Podemos encontrar el área bajo una curva utilizando la integración definida. Pero ¿podremos calcular el volumen de la forma tridimensional que se genera al girar la sección de una curva sobre uno de los ejes (o sobre cualquier línea horizontal o vertical)? Este es un viejo tutorial que ahora está incluido en otros tutoriales. Sin embargo, te dará una herramienta poderosa y ¡te hará estirar tus poderes de visualización en 3D!