Khan Academy on a Stick
Derivadas parciales, gradiente, divergencia, rotacional
Pensando en las formas de las derivadas en varias dimensiones y en funciones vectoriales: derivadas parciales, gradiente, divergencia y rotacional.
-
 Derivadas parciales
(ES)
cc
Derivadas parciales
(ES)
ccIntroducción a las derivadas parciales.
-
 Derivadas parciales 2
(ES)
cc
Derivadas parciales 2
(ES)
ccMás sobre derivadas parciales
Derivadas parciales
Vamos a saltar de ese aburrido mundo en 2D (bueno, que no era tan aburrido después de todo), al apasionante mundo tridimensional en el que todos vivimos y respiramos. En lugar de funciones de x que pueden visualizarse como rectas, podemos tener funciones de x y y que pueden visualizarse como superficies. Pero, ¿la idea de derivada todavía tiene sentido? ¡Por supuesto que sí! Siempre que especifiques en qué dirección vas ¡Bienvenido al mundo de las derivadas parciales!
-
 Gradiente 1
(ES)
cc
Gradiente 1
(ES)
ccIntroducción al gradiente
-
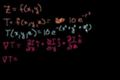 Gradiente de un campo escalar
(ES)
cc
Gradiente de un campo escalar
(ES)
ccIntuición del gradiente de un campo escalar (la temperatura en una habitación) en 3 dimensiones.
Gradiente
Alguna vez caminaste sobre una colina y te preguntaste cuál sería la forma más rápida para bajar (o para subir). Ahora puedes averiguar esto exactamente con el uso del gradiente.
-
 Divergencia 1
(ES)
cc
Divergencia 1
(ES)
ccIntroducción a la divergencia de un campo vectorial.
-
 Divergencia 2
(ES)
cc
Divergencia 2
(ES)
ccIntuición sobre los que es la divergencia de un campo vectorial.
-
 Divergencia 3
(ES)
cc
Divergencia 3
(ES)
ccAnalizando un campo vectorial utilizando su divergencia.
Divergencia
¿Las líneas de un campo vectorial están "acercándose" o "separándose" en un punto determinado en el espacio? La divergencia es un operador vectorial que nos da como resultado un valor escalar para cualquier punto en un campo vectorial. Si es positivo, entonces el campo vectorial diverge. De lo contrario, converge
-
 Divergencia 1
(ES)
cc
Divergencia 1
(ES)
ccIntroducción a la divergencia de un campo vectorial
-
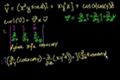 Divergencia 2
(ES)
cc
Divergencia 2
(ES)
ccLa mecánica de calcular la espiral.
-
 Divergencia 3
(ES)
cc
Divergencia 3
(ES)
ccMás de la divergencia
Rotacional
El rotacional mide qué tanto un campo vectorial está "girando". Un poco de doloroso de calcular, pero será útil más tarde cuando trabajemos con los teoremas de Stokes y de Green.