Khan Academy on a Stick
Exponentes, radicales y notación científica
Entender y resolver exponentes sin el uso del álgebra.
-
 Introducción a los exponentes
(EN)
Introducción a los exponentes
(EN)
-
 Elevando a un número a la décima y primera potencia
(EN)
Elevando a un número a la décima y primera potencia
(EN)
-
 Potencias de 1 y -1
(EN)
Potencias de 1 y -1
(EN)
-
 Potencias de fracciones
(EN)
Potencias de fracciones
(EN)
-
 Potencias de cero
(EN)
Potencias de cero
(EN)
-
 Exponente ejemplo 1
(EN)
cc
Exponente ejemplo 1
(EN)
cc -
 Exponente ejemplo 2
(ES)
cc
Exponente ejemplo 2
(ES)
cc
El mundo de los exponentes
La suma fue interesante. La multiplicación aún más. ¿Estás con ánimo para aprender una nueva operación que hace crecer los números aún más rápido? ¿Alguna vez pensaste que se podía expresar la multiplicación repetida muchas veces de una forma más corta? ¿Alguna vez has querido describir cómo las cosas en el universo crecen y decrecen? Bueno, ¡los exponentes son la respuesta! Este tutorial abarca desde lo básico de exponentes a exponentes negativos y fraccionarios. Se asume que aún recuerdas la multiplicación, los números negativos y las fracciones.
-
 Entendiendo las Raíces Cuadradas
(ES)
cc
Entendiendo las Raíces Cuadradas
(ES)
ccEntendiendo las Raíces Cuadradas
-
 Aproximando Raíces Cuadradas
(ES)
Aproximando Raíces Cuadradas
(ES)
Aproximando Raíces Cuadradas
-
 Simplifying square roots
(EN)
Simplifying square roots
(EN)
-
 Simplificando radicales
(ES)
cc
Simplificando radicales
(ES)
ccUtilizando las reglas de los exponente para simplificar radicales o raíces cuadradas
-
 Raíces Cuadradas y Números Reales
(EN)
Raíces Cuadradas y Números Reales
(EN)
-
 Sumando y simplificando Radicales
(ES)
Sumando y simplificando Radicales
(ES)
Más sobre Simplificación de Expresiones Radicales
The square root
Un contendiente fuerte para el símbolo más divertido e impresionante en las matemáticas es el radical. ¿Qué es? ¿Cómo se relaciona con los exponentes? ¿Cuál es la diferencia entre la raíz cuadrada y la raíz cúbica? ¿Cómo se pueden simplificar, multiplicar y sumar estas cosas? Para este tutorial debes conocer los fundamentos de los exponentes y las propiedades de los exponentes y te llevará a través del radical mundo de los radicales (y te da algo de practica en el camino).
-
 Encontrando Raíces Cúbicas
(ES)
cc
Encontrando Raíces Cúbicas
(ES)
ccEncontrando Raíces Cúbicas
-
 Cube root of a non-perfect cube
(EN)
Cube root of a non-perfect cube
(EN)
-
 Simplificando una raíz cúbica
(ES)
Simplificando una raíz cúbica
(ES)
Simplificando expresiones radicales 1
The cube root
If you're familiar with the idea of a square root, we're about to take things one step (dimension?) further with the cube root. This generally refers to finding a number that ,when cubed, is equal to the number that you're trying to find the cube root of!
-
 Ejercicio de patrones en ceros
(EN)
Ejercicio de patrones en ceros
(EN)
-
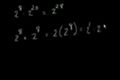 Reglas de los Exponentes Parte 1
(ES)
cc
Reglas de los Exponentes Parte 1
(ES)
ccIntroducción a las reglas de los exponentes
-
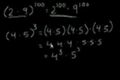 Reglas de los Exponentes Parte 2
(ES)
cc
Reglas de los Exponentes Parte 2
(ES)
cc2 reglas más de exponentes con una introducción a problemas compuestos
-
 Propiedades de los Exponente que Involucran Cocientes
(ES)
Propiedades de los Exponente que Involucran Cocientes
(ES)
Propiedades de los Exponente que Involucran Cocientes
Propiedades de los exponentes
¿Cansado de complicadas y peludas expresiones con exponentes? ¿Te sientes obligado a simplificarlas? Bien, este tutorial puede darte las herramientas necesarias. Si ya sabes un poco sobre exponentes, en este tutorial aprenderás mucho más mientras aprendes las reglas para simplificar exponentes.
-
 Exponentes negativos
(EN)
Exponentes negativos
(EN)
-
 Intuición sobre Exponentes Negativos
(ES)
cc
Intuición sobre Exponentes Negativos
(ES)
ccIntuición sobre por qué a^-b = 1/(a^b) (y por qué a^0 =1)
-
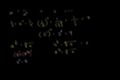 Exponentes Cero, Negativos y Fraccionales
(ES)
cc
Exponentes Cero, Negativos y Fraccionales
(ES)
ccExponentes Cero, Negativos y Fraccionales
-
 Exponentes fraccionados básicos
(EN)
Exponentes fraccionados básicos
(EN)
-
 Ejemplos de exponentes negativos fraccionados
(EN)
Ejemplos de exponentes negativos fraccionados
(EN)
-
 Ejemplos de exponentes negativos fraccionados 2
(EN)
Ejemplos de exponentes negativos fraccionados 2
(EN)
-
 Exponentes fraccionados con numeradores diferentes a 1
(EN)
Exponentes fraccionados con numeradores diferentes a 1
(EN)
Exponentes negativos y fraccionales
Normalmente es una mala idea juntarse con gente negativa o hacer cosas negativas, pero nosotros creemos que está bien asociarse con los exponentes negativos. Y las fracciones exponenciales son aún más divertidas. Esta idea abrirá nuevas visiones para tu vida matemática.
-
 Introducción a la notación científica
(EN)
cc
Introducción a la notación científica
(EN)
ccIntroducción a la notación científica. Una profunda discusión acerca del porque y como se utiliza la notación científica.
-
 Notación Científica
(ES)
Notación Científica
(ES)
Notación Científica
-
 Ejemplos de Notación Científica
(EN)
cc
Ejemplos de Notación Científica
(EN)
ccMás ejemplos de notación científica
-
 Notación Científica 1
(ES)
Notación Científica 1
(ES)
Notación Científica 1
-
 Ejemplo 2 de Notación Científica
(ES)
Ejemplo 2 de Notación Científica
(ES)
Notación Científica 2
Notación científica
Los científicos e ingenieros a menudo tienen que ocuparse de números super enormes (como 6,000,000,000,000,000,000,000) y super pequeños (como 0.0000000000532). ¿Cómo pueden hacer esto con sus manos sin cansarse? ¿Cómo pueden mirar un número y entender qué tan grande o pequeño es sin contar los dígitos? La respuesta es utilizar la notación científica. Si llegas a este tutorial con una comprensión básica de exponentes positivos y negativos, te va a dejar con una nueva apreciación de cómo se pueden representar números ¡realmente enormes y realmente pequeños!
Órdenes de magnitud
When people want to think about the general size of things but not worry about the exact number, they tend to think in terms of "orders of magnitude". This allows us to analyze and make comparisons between numbers very quickly, which allows us to make decisions about them quickly as well.
-
 Multiplicando en Notación Científica
(ES)
Multiplicando en Notación Científica
(ES)
u11_l1_t4_we_int Multiplicando en Notación Científica
-
 Ejemplo de multiplicación en notación científica
(EN)
Ejemplo de multiplicación en notación científica
(EN)
Ejemplo de multiplicación en notación científica
-
 Ejemplo de división de notación científica
(EN)
Ejemplo de división de notación científica
(EN)
Ejemplo que muestra como dividir dos números expresados en notación científica
-
 Multiplying and dividing in scientific notation
(EN)
Multiplying and dividing in scientific notation
(EN)
-
 Simplifying a complicated expression into scientific notation
(EN)
Simplifying a complicated expression into scientific notation
(EN)
-
 Calculating red blood cells in the body using scientific notation
(EN)
Calculating red blood cells in the body using scientific notation
(EN)
Computing with scientific notation
You already understand what scientific notation is. Now you'll actually use it to compute values and solve real-world problems.
 Ejercicio de órdenes de magnitud ejemplo 2
Ejercicio de órdenes de magnitud ejemplo 2