Khan Academy on a Stick
Triángulos rectángulos
Los triángulos no son siempre rectos (aunque nunca torcidos), pero cuando son triángulos rectángulos se abre un mundo apasionante de posibilidades. No es sólo que los triángulos rectángulos sean buena onda de nacimiento, sino que también son la base de ideas muy importantes de trigonometría y de geometría analítica (como la distancia que separa dos puntos en el espacio).
-
Teorema de Pitágoras
(ES)
Teorema de Pitágoras
-
La introducción a Teorema de Pitágoras
(ES)
Introducción al teorema de Pitágoras
-
Teorema de Pitágoras 1
(EN)
Teorema de Pitágoras 1
-
Teorema de Pitágoras 2
(EN)
Teorema de Pitágoras 2
-
Teorema de Pitágoras 3
(ES)
ccTeorema de Pitágoras 3
-
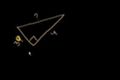Introducción al teorema de Pitágoras
(EN)
Triángulos rectángulos y el teorema de Pitágoras
-
Teorema de Pitágoras II
(ES)
ccMás ejemplos del teorema de Pitágoras. Introducción a los triángulos de 45-45-90.
Teorema de Pitágoras
Llamado así por el filósofo griego que vivió hace casi 2600 años, el Teorema de Pitágoras tiene todo lo que se le puede pedir a un teorema matemático (Pitágoras también inició un movimiento religioso). Es simple. Es hermoso. Es poderoso. En este tutorial estudiaremos qué es el teorema de Pitágoras y cómo puede usarse. Tenemos otro tutorial que te da todas las demostraciones de este teorema que puedas necesitar
-
La demostración de Garfield del Teorema de Pitágoras
(EN)
La demostración que dada por James Garfield del Teorema de Pitágoras.
-
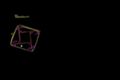La demostración de Bhaskara del Teorema de Pitágoras
(EN)
Una demostración visual elegante del Teorema de Pitágoras desarrollada por el matemático hindú del siglo 12 Bhaskara.
-
Demostración del Teorema de Pitágoras Usando Semejanza
(EN)
Prueba del Teorema de Pitágoras usando semejanzas
-
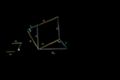Otra Demostración del Teorema de Pitágoras
(EN)
Visualmente, demostrar el Teorema de Pitágoras
Pruebas del Teorema de Pitágoras
El Teorema de Pitágoras es una de las ideas más famosas en las matemáticas. Este tutorial lo demuestra. Luego lo demuestra otra vez... y otra vez... y otra vez. Más allá de satisfacer cualquier escepticismo sobre si el Teorema de Pitágoras es o no verdad (sólo una prueba sería suficiente para eso), abrirá tu mente a nuevas y hermosas maneras de probar algo tan poderoso.
-
Demostración de la relación de lados de triángulos de 30-60-90
(ES)
Demostrando los cocientes entre los lados de un triángulo 30-60-90
-
Relación de los lados del triángulo de 45-45-90
(ES)
Mostrar que la proporción de los lados de un triángulo de 45-45-90 son 1:1:raíz cuadrada(2)
-
Ejemplo de un problema de un Triángulo 30-60-90
(ES)
Usar lo que sabemos sobre los triángulos de 30-60-90 para resolver lo que al principio pareciera ser un problema desafiante
-
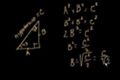Triángulos de 45-45-90
(ES)
Introducción a los triángulos de 45-45-90
-
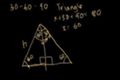Introducción a los Triángulos de 30-60-90
(ES)
Más ejemplos de 45-45-90 y una introducción a los triángulos de 30-60-90.
-
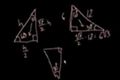Triángulos de 30-60-90 II
(ES)
Más ejemplos usando triángulos de 30-60-90.
Triángulos rectángulos especiales
Odiamos tener que escoger favoritos, pero realmente hay ciertos triángulos rectángulos que son más especiales que otros. En este tutorial te vamos a enseñar estos triángulos especiales, te mostraremos por qué son especiales, y ¡te lo vamos a demostrar! Se trata de triángulos de 30-60-90 y 45-45-90 (los números se refieren a la medida de los ángulos en el triángulo).