Khan Academy on a Stick
Estadística Inferencial
Inferecnias basadas en datos muestrales. Intervalos de confianza. Margen de error. Prueba de hipótesis.
-
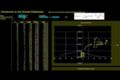 Introduction to the Normal Distribution
(ES)
Introduction to the Normal Distribution
(ES)
Explorando la distribución normal
-
 Distribución normal, ejercicio de Excel
(ES)
Distribución normal, ejercicio de Excel
(ES)
(Largo-26 minutos) Presentación en hoja de cálculo para mostrar que la distribución normal se aproxima a la distribución binomial para un gran número de ensayos.
-
 Problemas CK12.org de distribución normal: sentido cualitativo de distribuciones normales
(ES)
Problemas CK12.org de distribución normal: sentido cualitativo de distribuciones normales
(ES)
Discusión acerca de qué tan "normal" podría ser una distribución
-
 CK12.org problemas de distribución normal: regla empírica
(ES)
CK12.org problemas de distribución normal: regla empírica
(ES)
El uso de la regla empírica (o regla 68-95-99.7 ) para estimar las probabilidades de distribuciones normales
-
 CK12.org problemas con la distribución normal: valores z
(ES)
CK12.org problemas con la distribución normal: valores z
(ES)
Práctica con los valores de Z
-
 Ejercicio CK12.org : distribución normal estándar y la regla empírica
(ES)
Ejercicio CK12.org : distribución normal estándar y la regla empírica
(ES)
El uso de la regla empírica con una distribución normal estándar
-
 Práctica CK12.org: más de la regla empírica y los valores Z
(ES)
Práctica CK12.org: más de la regla empírica y los valores Z
(ES)
Más práctica sobre la regla empírica y los valores Z
Distribución normal
La distribución normal (a menudo denominada la "curva de campana") está en el centro de la mayor parte de la estadística inferencial. Asumiendo que los procesos más complejos sueelen tener una distribución normal (vamos a ver por qué asumir esto es razonable), podemos estimar la probabilidad de que ocurra por azar. Para disfrutar mejor este tutorial, es bueno entender las distribuciones de probabilidad y las variables aleatorias. También debe estar muy familiarizado con las nociones de media poblacional y muestral y la desviación estándar.
-
 Teorema del Límite Central
(ES)
cc
Teorema del Límite Central
(ES)
ccIntroducción al terorema del limite central y la distribución muestral de la media
-
 Distribución muestral de la media de la muestra
(ES)
Distribución muestral de la media de la muestra
(ES)
El Teorema de límite central y la distribución muestral de la media de la muestra
-
 Distribución de la media de la muestral 2
(ES)
Distribución de la media de la muestral 2
(ES)
Más sobre el Teorema del límite Central y la distribución de la media muestral
-
 Error estándar de la media
(ES)
cc
Error estándar de la media
(ES)
ccError estándar de la media (también conocido como la desviación estándar de la distribución muestral de la media muestral!)
-
 Problema de ejemplo de la distribución muestral
(ES)
Problema de ejemplo de la distribución muestral
(ES)
Averiguar la probabilidad de quedarse sin agua en un viaje de campamento
Distribución muestral
En este tutorial, experimentamos una de las ideas más interesantes en el Teorema de límite central de la estadística. Sin él, sería mucho más difícil hacer cualquier inferencia acerca de los parámetros de la población a partir de los estadísticos de la muestra. Establece que, independientemente de cómo sea la distribución de la población, la distribución de los media muestral (usted aprenderá lo que esto significa) puede ser una distribución normal. Es una buena idea entender un poco acerca de distribuciones normales antes de sumergirse en este tutorial.
-
 Intervalo de Confianza 1
(ES)
cc
Intervalo de Confianza 1
(ES)
ccEstimación de la probabilidad de que la media poblacional esté en un rango alrededor de la media muestral.
-
 Ejemplo de intervalo de confianza
(ES)
Ejemplo de intervalo de confianza
(ES)
Ejemplo de intervalo de confianza
-
 Intervalos de confianza de muestras pequeñas
(ES)
Intervalos de confianza de muestras pequeñas
(ES)
La construcción de intervalos de confianza con muestraspequeñas usando las distribuciones t
Intervalos de confianza
Todos tenemos los intervalos de confianza ("yo soy el rey del mundo!") y intervalos de no-confianza ("nadie me ama"). No es lo que este tutorial trata. Este tutorial toma lo que ya conoces del Teorema de límite central, las distribuciones muestrales y los valores z y utiliza estas herramientas para bucear en el mundo de la estadística inferencial. Al principio puede parecer mágico, pero partiendo de nuestra muestra, ahora podemos hacer inferencias acerca de la probabilidad de que la media de la población esté dentro de un intervalo.
-
 Ejemplo de media y varianza de la distribución de Bernoulli
(ES)
Ejemplo de media y varianza de la distribución de Bernoulli
(ES)
Ejemplo de media y varianza de la distribución de Bernoulli
-
 Fórmulas de la media y varianza de la Distribución de Bernoulli
(ES)
Fórmulas de la media y varianza de la Distribución de Bernoulli
(ES)
Fórmulas de la media y varianza de la Distribución de Bernoulli
-
 Margen de Error 1
(ES)
Margen de Error 1
(ES)
Encontrar el intervalo de confianza del 95% para la proporción de la población que vota por un candidato.
-
 Margen de Error 2
(ES)
Margen de Error 2
(ES)
Encontrar el intervalo de confianza del 95% para la proporción de la población que vota por un candidato.
Distribución de Bernoulli y margen de error
Alguna vez se preguntó a qué se refieren los encuestadores cuando dicen que hay un 3% "margen de error" en sus resultados. Bueno, este tutorial no sólo explicará lo que significa, sino que le proporcionará las herramientas y la comprensión necesarias para que usted mismo sea un encuestador!
-
 Prueba de hipótesis y p-valores
(ES)
Prueba de hipótesis y p-valores
(ES)
Prueba de hipótesis y p-valores
-
 Pruebas de una cola y de dos colas
(ES)
cc
Pruebas de una cola y de dos colas
(ES)
ccPruebas de una cola y de dos colas
-
 Errores tipo 1
(ES)
Errores tipo 1
(ES)
Errores tipo 1
-
 El estadístico Z vs. el estadístico T
(ES)
El estadístico Z vs. el estadístico T
(ES)
El estadístico Z vs. el estadístico T
-
 Prueba de hipótesis para una muestra pequeña
(ES)
Prueba de hipótesis para una muestra pequeña
(ES)
Prueba de hipótesis para una muestra pequeña
-
 Intervalo de confianza del estadístico T
(ES)
Intervalo de confianza del estadístico T
(ES)
Estadístico T; intervalo de confianza (para tamaños de muestra pequeños)
-
 Prueba de hipótesis de la proporción en muestras grandes
(ES)
Prueba de hipótesis de la proporción en muestras grandes
(ES)
Prueba de hipótesis de la proporción en muestras grandes
Prueba de hipótesis con una muestra
Este tutorial nos ayuda a responder a una de las preguntas más importantes, no sólo en estadística, sino de toda la ciencia: qué tan seguros podemos estar de que el resultado de un nuevo medicamento o proceso no es por azar sino debido al su verdadero impacto. Si usted está familiarizado con las distribuciones muestrales y los intervalos de confianza, entonces está listo para esta aventura!
-
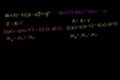 Varianza de las diferencias de Variables aleatorias
(ES)
Varianza de las diferencias de Variables aleatorias
(ES)
Varianza de las diferencias de Variables aleatorias
-
 Distribución de la diferencia de las medias muestrales
(ES)
cc
Distribución de la diferencia de las medias muestrales
(ES)
ccDistribución de la diferencia de las medias muestrales
-
 Intervalo de confianza de la diferencia de medias
(ES)
Intervalo de confianza de la diferencia de medias
(ES)
Intervalo de confianza de la diferencia de medias
-
 Aclaración sobre el intervalo de confianza de la diferencia de medias
(ES)
cc
Aclaración sobre el intervalo de confianza de la diferencia de medias
(ES)
ccAclaración sobre el intervalo de confianza de la diferencia de medias
-
 Prueba de hipótesis para diferencia de medias
(ES)
Prueba de hipótesis para diferencia de medias
(ES)
Prueba de hipótesis para diferencia de medias
-
 Comparación de proporciones poblacionales 1
(ES)
Comparación de proporciones poblacionales 1
(ES)
Comparación de proporciones poblacionales 1
-
 Comparación de proporciones poblacionales 2
(ES)
Comparación de proporciones poblacionales 2
(ES)
Comparación de proporciones poblacionales 2
Prueba de hipótesis con dos muestras
Ya estás familiarizado con la prueba de hipótesis con una muestra . En este tutorial, iremos más allá al comprobar si la diferencia entre las medias de dos muestras parece inverosímil que sea sólo debido al azar.
-
 Introducción a la distribución Ji-cuadrada
(ES)
Introducción a la distribución Ji-cuadrada
(ES)
Introducción a la distribución Ji-cuadrada
-
 Prueba de la Ji cuadrada de Pearson (bondad de ajuste)
(ES)
Prueba de la Ji cuadrada de Pearson (bondad de ajuste)
(ES)
Prueba de la Ji cuadrada de Pearson (bondad de ajuste)
-
 Prueba de cuadro de contingencia de la Ji-cuadrada
(ES)
Prueba de cuadro de contingencia de la Ji-cuadrada
(ES)
Prueba de cuadro de contingencia de la Ji-cuadrada
Distribución de probabilidad Chi-cuadrada
Usted se ha vuelto bueno en la prueba de hipótesis al hacer suposiciones sobre las distribuciones subyacentes. En este tutorial, aprenderemos acerca de una nueva distribución (la ji-cuadrada) e incluso cómo puede ayudarle (sí, a usted) a inferir qué es una distribución subyacente!
-
 ANOVA 1 - Cálculo de STC (Suma Total de Cuadrados)
(ES)
cc
ANOVA 1 - Cálculo de STC (Suma Total de Cuadrados)
(ES)
ccAnálisis de Varianza 1 - Cálculo de STC (Suma Total de Cuadrados)
-
 ANOVA 2 - cálculo STC y DEC (suma total de cuadrados y suma de cuadrados dentro y entre) .avi
(ES)
ANOVA 2 - cálculo STC y DEC (suma total de cuadrados y suma de cuadrados dentro y entre) .avi
(ES)
Análisis de varianza 2 - cálculo SSW y SSB (suma total de cuadrados dentro y entre) .avi
-
 ANOVA 3 - prueba de hipótesis con el estadístico F
(ES)
ANOVA 3 - prueba de hipótesis con el estadístico F
(ES)
Análisis de varianza 3 - prueba de hipótesis con el estadístico F
Análisis de la varianza
Ya sabes bastante sobre pruebas de hipótesis con una o dos muestras. Ahora vamos más allá al hacer inferencias basadas en tres o más muestras. Vamos a usar la muy especial distribución F (F significa "fabulosa").