Khan Academy on a Stick
Transformada de Laplace
Transformaciones y la transformación de Laplace en particular. Convoluciones integrales.
-
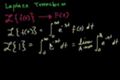Transformada de Laplace 1
(ES)
ccIntroducción a la transformada de Laplace
-
Transformada de Laplace 2
(ES)
ccTransformada de Laplace de e^at
-
L{sen(at)}) - transformada de sen(at)
(ES)
ccTransformada de Laplace de sen(at) (parte 1)
-
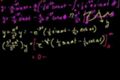Parte 2 de la transformación de sin(at)
(ES)
ccParte 2 de obtener la transformación de Laplace de sin(at)
Transformada de Laplace
Ahora podemos usar una de las mejores técnicas en matemáticas para transformar ecuaciones diferenciales en algebraicas. ¡También aprenderás acerca de transformaciones en general!
-
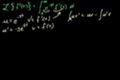Laplace como operador lineal y Laplace de derivadas
(ES)
ccPropiedades útiles de la transformada de Laplace
-
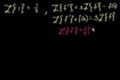Transformada de Laplace de cos t y polinomios
(ES)
cc¡Transformada de Laplace de coseno y polinomios!
-
Transformación de "desplazamiento" por la función de multiplicación de exponencial
(ES)
ccUna bolsa de cosas para saber acerca dela transformada de Laplace.
-
Transformada de Laplace de: L{t}
(ES)
ccDeterminando la transformada de Laplace de t
-
Transformada de Laplace de t^n: L{t^n}
(ES)
ccTransformada de Laplace de t^n: L{t^n}
-
La transformación Laplace de la función de la unidad de un paso
(ES)
ccIntroducción a la función de un paso y la transformación de Laplace
-
Ejemplos de la inversa de Laplace
(ES)
ccUsando nuestro kit de herramientas para tomar algunas inversas de la transformada de Laplace
-
Función Delta de Dirac
(ES)
ccIntroducción a la función Delta de Dirac
-
Transformada de Laplace de la función Delta de Dirac
(ES)
ccAveriguando la transformada de Laplace de la función Delta de Dirac
Propiedades de la transformada de Laplace
Sabes como utilizar la definición de la transformada de Laplace. En este tutorial exploraremos algunas de las propiedades de la transformada que comenzaran a dejar en claro por qué son tan útiles para la ecuaciones diferenciales. Este tutorial esta bien emparejado con el tutorial sobre usar "Transformada de Laplace para resolver ecuaciones diferenciales". De hecho puede que regreses a este tutorial una y otra vez mientras resuelvas más y más problemas.
-
La transformada de Laplace para resolver una ecuación
(ES)
ccUsando la transformada deLaplacepara resolver una ecuación que ya sabíamos como resolver.
-
La transformada de Laplace soluciona una ecuación 2
(ES)
ccSegunda parte de usar la transformada de Laplace para resolver una ecuación diferencial.
-
Usar la transformación de Laplace para resolver una ecuación no homogénea
(ES)
ccResolviendo una ecuación diferencial no homogénea usando la transformada de Laplace
-
Ecuación diferencial de la función de un paso/Laplace
(ES)
ccEcuaciones diferenciales complicadas implican una función de un paso en la que nosotros usamos la transformación de Laplace para resolver.
Transformada de Laplace para resolver una ecuación diferencial
Sabes un poco acerca de tomar transformadas de Laplace y propiedades útiles de la transformada. Te mueres por aplicar estas habilidades en una ecuación diferencial de verdad. ¡No esperes más!
-
Introducción a la convolución
(ES)
ccIntroducción a la convolución
-
La convolución y la transformada de Laplace
(ES)
ccEntendiendo como se relaciona el producto de las transformaciones de dos funciones con su convolución.
-
Usar el Teorema de Convolución para resolver una prueba de valor inicial
(ES)
ccUtilizando el Teorema de convolución para resolver un problema de valor inicial
La convolución integral
Este tutorial no será convolucionado como tú podrías esperar. Veremos lo que las multiplicaciones transforman en el dominio de s que nos da el dominio del tiempo.